Euclid's elements, 300 BC: updated ⊙2012 ⊘12 ⊖20

ike-radi-formula

appearance range-slider-skin version 0.04

radius
ikeRadi
analytical
numerical
evaluation
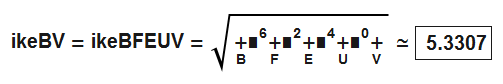
graphical
interpretation

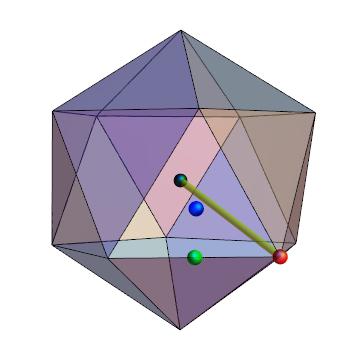
notation (under reconstruction)




all results for comparing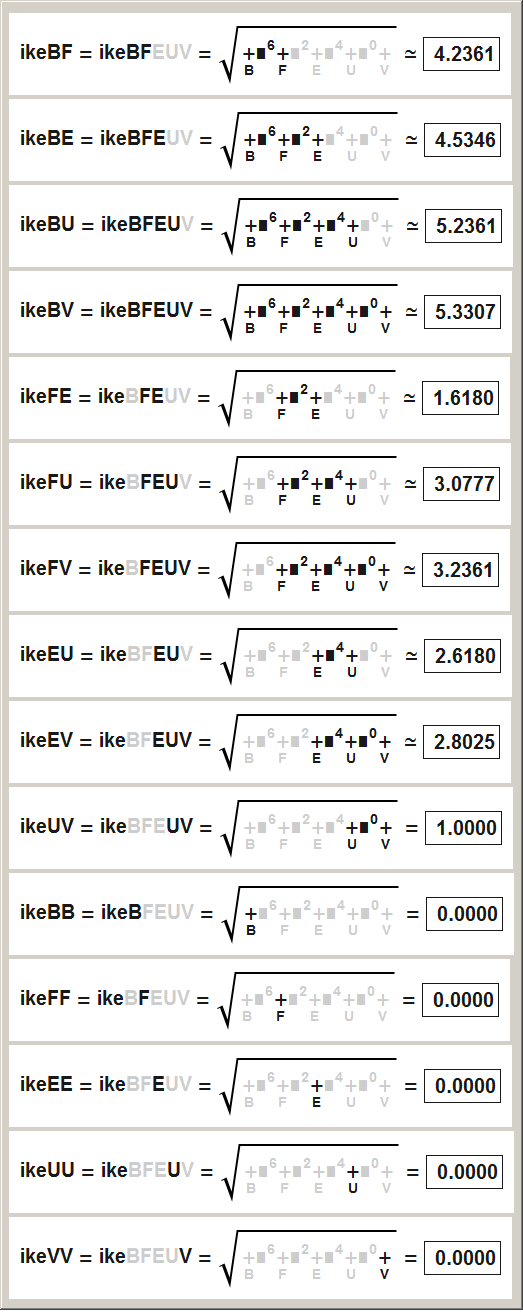

doe


reflections on radi-mindmaps

Three new ideas are concentrated in a beautiful mindmap.

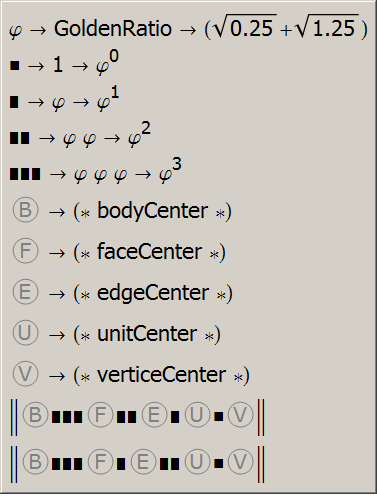
Idea1: The introduction and usage of a referenceSystem, which comes along with {B, F, E, U, V}. ReferenceSystems do not contribute any values, like drawing a function in a 2D-ReferenceSystem, but they are necessary for human "orientation".

Idea2: The introduction of the UnitSphere with a radius set to 1, the "neutral element of multiplication", allows a "high quality" analytical setup. Now a teenager can remember a set of radi without the need of calculations or searching in tables. He will do calculations far faster than those who ignore the mindmap. Another analytical advantage is: we can jump simply from doeRadi to ikeRadi. The UnitSphere could be put on other places to produce other mindmaps, an example will be given for doeRadi.

Idea3: The names can be used now as mathematical objects. ikeBV is far better then "circumRadius of Icosahedron", because we can calculate with it. Example: ikeBE²+ikeEV²=ikeBV², or ikeFE²+ikeEV²=ikeFV². And the new nameSystem is extendable and shorter, simply more "mathematical". Two advantages: calculatable and extendable.


appearance sky-scraper-skin version 0.01

Sky-scraper-skin range-selection is done by underline. A good and simple version suitable for explanations at school, since underlining can be repeated.

doe


legend and notation summary


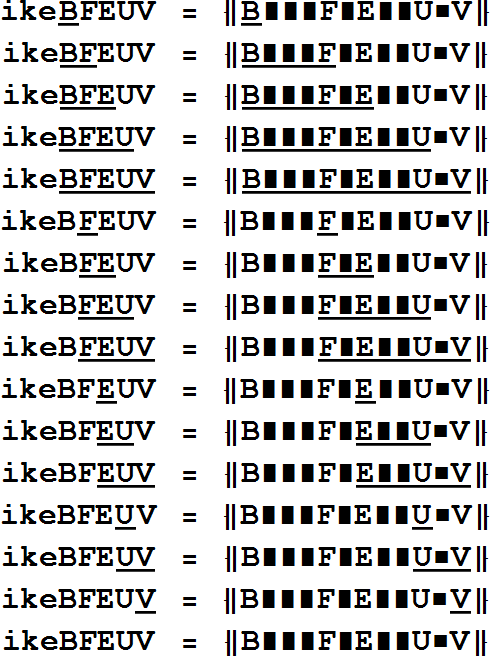
appearance exponent-skin version 0.01

Comparing ikeRadi and doeRadi, without radi which evaluate to zero. Although exponent-skin has lower quality than range-slider-skin, ignoring the referenceSystem BFEUV, it appears very compactly.

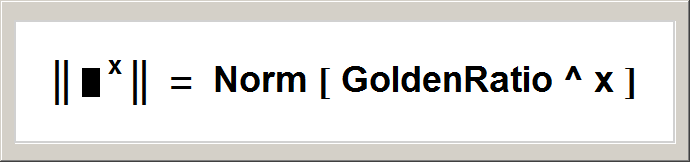
Notation hints: The black rectangle is a GoldenRatio rectangle, used as a natif identifier for the GoldenRatio constant. The exponents written in gray are "disabled values" and can be ignored. They are printed only for visualizing the symmetry. The bracing verticalBars denote the "Norm" symbol. Surprising: the results could be arranged in a tetrahedral form.



first dodecahedron & icosahedron radius formula worldwide // attention: unrevised material, never seen by any mathematician, nor an English lector // first upload ⊙2012 ⊘12 ⊖20 // discovered by // internetpseudo // hieronymous-le-clochard

Mathematical aspect: A single recursion is responsible for all radii, responsible for both the ikeRadi and the doeRadi. For doeRadii the recursion goes: GoldenRatio^n + GoldenRatio^(n+1) → GoldenRatio^(n+2), for ikeRadii the recursion goes: GoldenRatio^n -GoldenRatio^(n+2) → -GoldenRatio^(n+1), and this is just an algebraic exchange of two terms referencing the same recursionEquation.


A quick & dirty explanation would be:
doe&ikeRadii are normedSubranges @ phiRecursions. (phi=GoldenRatio)

The notation puzzle is just a temporary solution. A better version will come soon. Can a natif speaker correct my pages?

© 2012-2013   hieron@phimath.net   All rights reserved.
Website under construction!