Fibonacci dances with 999899.99 mathematicians

doe-radi-formula

appearance range-slider-skin version 0.04

radius
doeRadi
analytical
numerical
evaluation
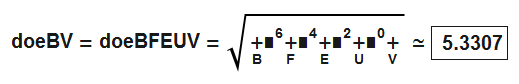
graphical
interpretation

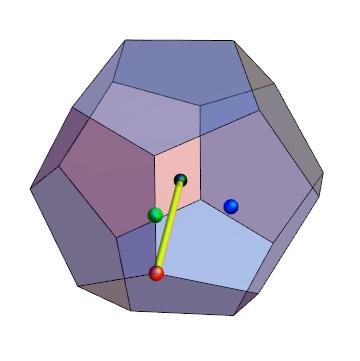
all results for comparing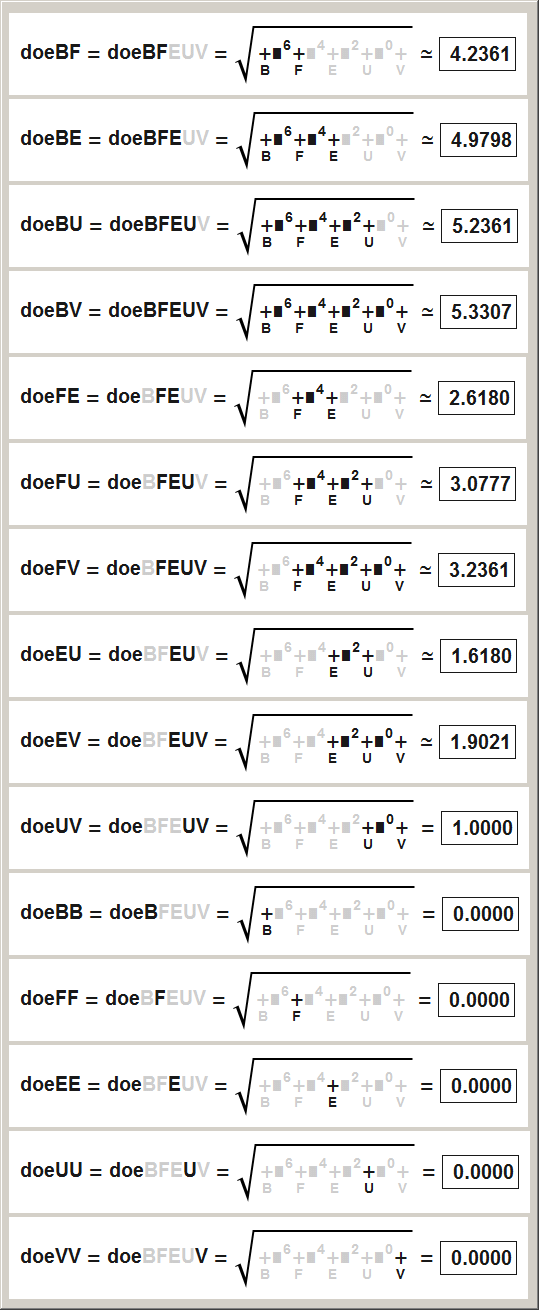

doe radi: just another try

worse or better?

doe
doe
doe




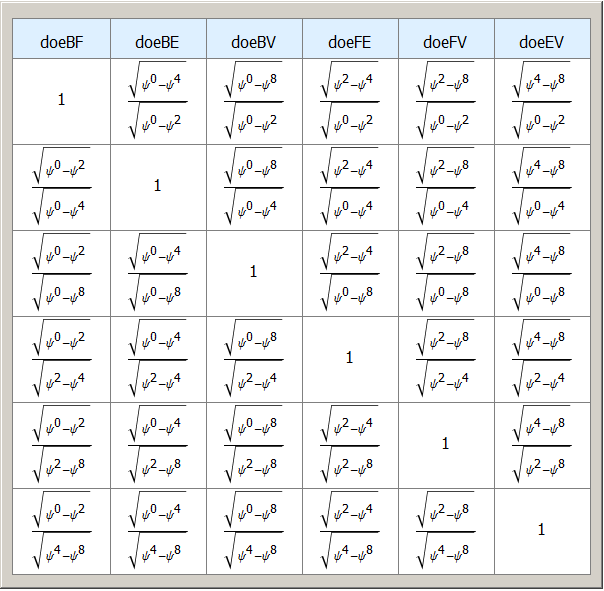
appearance sky-scraper-skin version 0.01

Sky-scraper-skin effects range-selection by underlining. A good and simple version suitable for explanations at school, since underlining can be repeated.






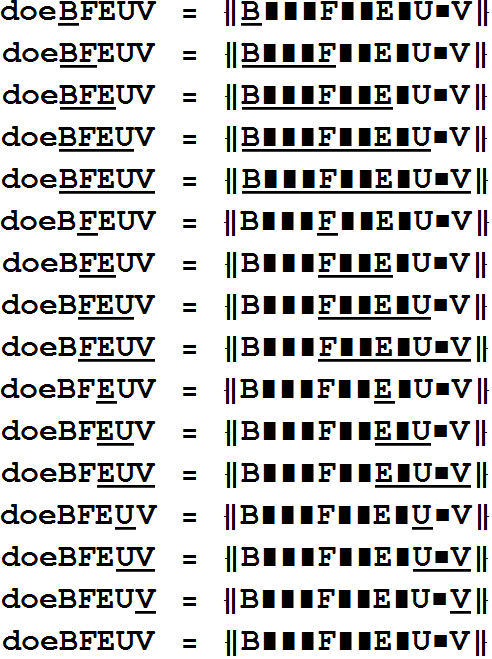
appearance baseform version 0.01

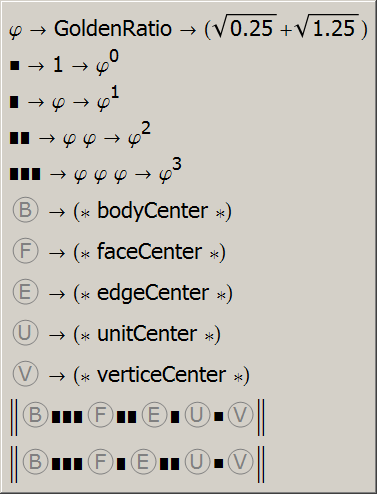
Representing numbers based at GoldenRatio² allows a fairly short notation for dodecahedron radi and icosahedron radi. In mathematics the following notation form is commonly used for numbers with a different base:

For example "5" written in binary base gives 1012 = 5. This means our "number base", has changed from default base to binary base. Using now the baseform with base GoldenRatio², denoted as φ², gives 101φ² = φ4 + 1. For the following two tables ...

"number base" → "GoldenRatio²" → φ² = (3+√5)/2 ≈ 2.618…


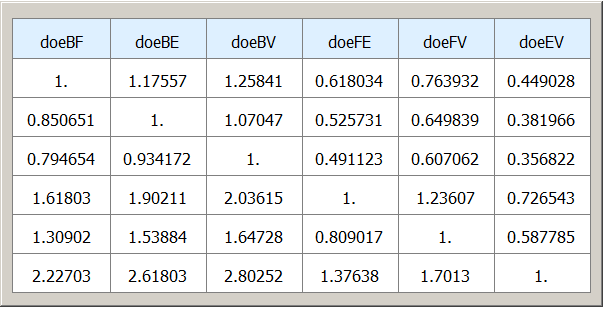
dodecahedron radi based GoldenRatio²

"dodecahedron radius from body center to   face center" → doeBF = √1000φ²
"dodecahedron radius from body center to   edge center" → doeBE = √1100φ²
"dodecahedron radius from body center to   unit center" → doeBU = √1110φ²
"dodecahedron radius from body center to vertex center" → doeBV = √1111φ²
"dodecahedron radius from face center to   edge center" → doeFE = √0100φ²
"dodecahedron radius from face center to   unit center" → doeFU = √0110φ²
"dodecahedron radius from face center to vertex center" → doeFV = √0111φ²
"dodecahedron radius from edge center to   unit center" → doeEU = √0010φ²
"dodecahedron radius from edge center to vertex center" → doeEV = √0011φ²
"dodecahedron radius from unit center to vertex center" → doeUV = √0001φ²


icosahedron radi based GoldenRatio²

"icosahedron radius from body center to   face center" → ikeBF = √1000φ²
"icosahedron radius from body center to   edge center" → ikeBE = √1010φ²
"icosahedron radius from body center to   unit center" → ikeBU = √1110φ²
"icosahedron radius from body center to vertex center" → ikeBV = √1111φ²
"icosahedron radius from face center to   edge center" → ikeFE = √0010φ²
"icosahedron radius from face center to   unit center" → ikeFU = √0110φ²
"icosahedron radius from face center to vertex center" → ikeFV = √0111φ²
"icosahedron radius from edge center to   unit center" → ikeEU = √0100φ²
"icosahedron radius from edge center to vertex center" → ikeEV = √0101φ²
"icosahedron radius from unit center to vertex center" → ikeUV = √0001φ²

first dodecahedron & icosahedron radius formula worldwide // attention: unrevised material, never seen by any mathematician, nor an English lector // first upload ⊙2012 ⊘12 ⊖20 // discovered by hieronymous-le-clochard

Mathematical aspect: A single recursion is responsible for all radii, responsible for both the ikeRadi and the doeRadi. For doeRadii the recursion goes: GoldenRatio^n + GoldenRatio^(n+1) → GoldenRatio^(n+2), for ikeRadii the recursion goes: GoldenRatio^n -GoldenRatio^(n+2) → -GoldenRatio^(n+1), and this is just an algebraic exchange of two terms referencing the same recursionEquation.

A quick & dirty explanation would be:
doe&ikeRadii are normedSubranges @ phiRecursions. (phi=GoldenRatio)

© 2012-2013   hieron@phimath.net   All rights reserved.
Website under construction!